2024年国考数量关系备考技巧：几何特性

【导读】国家公务员考试网 同步海南华图发布： 2024年国考数量关系备考技巧：几何特性。 联系我们：0898-66769773。 更多公考资讯请关注公众号“海南华图”(hnhtsydw) 和 欢迎添加客服咨询

扫码加入
24年国考备考交流群

　　几何问题是数量关系中非常重要的题型，无论是国考还是省考，逢考必出，因此考生需要重点掌握。几何问题分为几何计算、几何特性等题型，几何计算类题目主要运用基本公式解题，考生需要熟记一些常用的公式，几何特性类题目主要运用几何特性去解题，常用的几何特性包括相似图形的尺寸扩大理论和几何最值定理，今天图图老师就带着大家一起学习一种常考的几何特性——相似图形的尺寸扩大理论。

　　【理论知识】

　　相似图形的尺度扩大理论：若将一个图形尺寸扩大为原来的N倍，对应角度不变;对应周长变为原来的N倍;面积变为原来的𝑁2倍;体积变为原来的𝑁3倍。

　　几何问题中有些题目用基本公式解题非常麻烦，如果可以用相似图形的尺寸扩大理论去解题，题目就会变得非常简单，比如下面这两个题目。

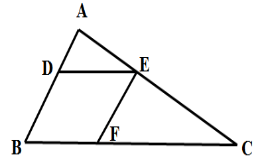
　　【例1】一块三角形农田ABC(如下图所示)被DE、EF两条道路分为三块。已知BD=2AD，CE=2AE，CF=2BF，则三角形ADE、三角形CEF和四边形BDEF的面积之比为：( )

A.1:3:3

　　B.1:3:4

　　C.1:4:4

　　D.1:4:5

　　【答案】C

　　【解析】第一步，本题考查几何问题，属于几何特殊性质类。

　　第二步，由BD=2AD，CE=2AE，CF=2BF，则DE∥BC，EF∥AB，即四边形BDEF是平行四边形，可得BD=EF，DE=BF。△ADE、△EFC和△ABC相似，符合相似图形的尺寸扩大理论，

　　△EFC的边长是△ADE的2倍，面积是△ADE的22=4倍，则△ADE和△CEF的面积之比是1:4。由BD=2AD，可知AB=3AD，△ABC的边长是△ADE的3倍，面积是△ADE的32=9倍，

　　则三角形ADE、三角形CEF和四边形BDEF的面积之比为：1:4:4。

　　因此，选择C选项。

　　【例2】某甜品店出售一种规则球形的甜品，该甜品由内部中空的球形面皮(每立方厘米成本0.4元)和实心的芝士球(每立方厘米成本1元)组成。无论甜品大小规格如何，其中的芝士球半径始终为甜品半径的四分之三。已知制作半径为1厘米的该甜品成本约为2.73元，那么要制作半径为2厘米的该甜品，成本约为：

　　A. 5.46元

　　B. 7.45元

　　C. 14.92元

　　D. 21.88元

　　【答案】D

　　【解析】第一步，本题考查几何问题，属于几何特殊性质类。

　　第二步，球体体积之比等于半径之比的立方，半径2厘米甜品的体积为半径1厘米甜品体积的2³=8倍，因此制作半径为2厘米甜品的成本为半径1厘米甜品的8倍。

　　第三步，成本约为2.73×8=21.84(元)。

　　因此，选择D选项。

　　从上面这两个例题就可以看出，有些题目如果用基础公式去解题，会非常复杂，尤其第二道题目，但是如果用相似图形的尺寸扩大理论解题就会大大减少计算量，加快做题速度。

公考预约：2024年国考公告预约 | 2024年国考模考大赛
网课学习：2024年公考核心课程 | 更多网络课程
面授课程：2024国家公务员考试笔试课程 | 备考咨询
图书推荐：2024年海南公考【暑假作业】 （电子版） | 2024版国家公务员录用考试专用教材（行测+申论） 教材+真题 4本
备考助力：2024年国家公务员笔试礼包【领航计划3.0】海南

　　——推荐阅读——

　　招录信息——2024国家公务员考试公告 | 职位查询 | 考试大纲 | 历年考情汇总

　　考生通道——2024国家公务员考试报名入口 | 准考证打印入口

　　报考备考——2024海南省公务员历年试题 | 历年试题 | 成绩查询

　　教材资料——2024国家公务员图书教材 | 每日一练

　　辅导课程——2024国家公务员考试笔试课程 | 网校课程 |  24国考模考大赛

　　更多2024国家公务员考试信息，敬请关注国家公务员考试网 / 海南公务员考试网。

　　最后图图预祝各位考生都能在2024年国家公务员考试中取得满意的成绩，成功上岸~

官方微信号

官方小程序